物理学におけるアルケー（ホーキング=ハートルの無境界仮説）

さて、奥行きとしての4次元のアルケーについて神秘学的に語るのは、この辺で一旦止めにして、現代宇宙論においてこの「アルケー（宇宙の始まり）」がどのように考えられているか、それについても紹介しておきましょう。現代宇宙論の主流は周知のようにビッグバン理論にあります。ビックバン理論によれば、宇宙は約137億年前に特異点という極微の点から突如、インフレーションという急速な膨張を起こしし、そこから大爆発を起こして誕生し、今尚、地球から330万光年離れるごとに秒速73kmを加算した形（ハッブル定数と言います）で膨張し続けていると言われています。しかし、この宇宙の開始点とされる特異点の存在は、物理学者たちにとっては甚だ目障りな存在です。特異点というのは、アインシュタインの宇宙方程式から必然的に導き出されてくるものらしいのですが、そこではエネルギー密度や温度が無限大になってしまうというのです。そのため、どんな方程式を立てようが計算不能になってしまい、物理法則はすべて破綻してしまいます。宇宙がどのようにして始まったのか何とか理性の力でイメージしたい物理学者たちにとっては、これはのっぴきならない事態です。

この厄介物の特異点を何とか回避できないかものかと考えたのが、あの車椅子の天才と言われたS（スティーブン）・ホーキングです。ホーキングは1983年にJ（ジェームス）・ハートルとともにに「無境界仮説」という奇抜な仮説を発表しました。無境界仮説は、この実時間の宇宙の開始以前に虚時間宇宙（量子重力期とも呼ばれます）というものが存在したのだと考え、ビッグバン以前の宇宙がどういう状態にあったかその有り様を数学的に示したのです。というのも、虚時間itを4次元不変距離の式に導入すると、時間と空間の区別が無効となり、特異点自体が消失してしまうからです。

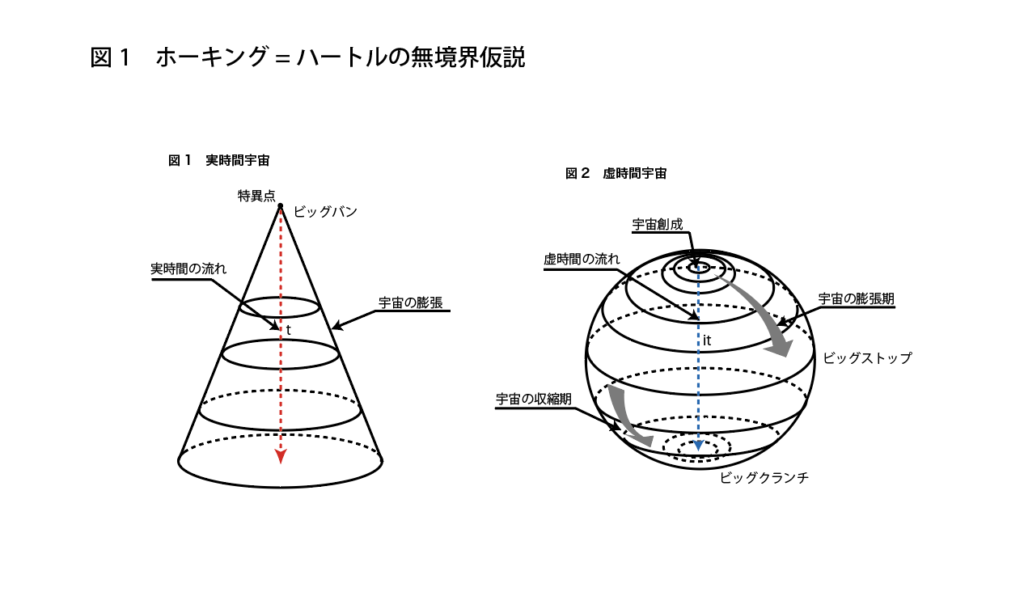
　このへんの事情を分りやすく説明すると、おおよそ下のような直観的な図で説明することができます。下図1で示したのが膨張宇宙と思って下さい。時間tと共に膨張していく姿をこの図では円錐形で示しています。円錐形の先はツンととんがっていますが、この先端点が特異点になっていると考えましょう。 

ここで、4次元不変距離の式における時間の項を虚時間it（時間tの項に虚数iを掛ける）にすると次のようになります。

ローレンツ変換の不変量である4次元距離をsとすると、

s²= (x²+y²+z²)+(ict)²

ここで実時間tの代わりに虚時間itを代入すると、

s²= (x²+y²+z²)+(ic・it)²

となり、 sを1と置いて整理すると

s²= (x²+y²+z²)+ (ct)² =1

という式になります。この式は4次元ユークリッド空間上での原点から1の距離を持つ3次元球面を表わす式と何ら変わるところはありません。つまり、時空を表す式に虚時間itを代入すると、4次元時空は4次元空間と区別がつかないものになってしまうということです。 

この実時間tから虚時間itへの変換（物理学ではウィック回転と呼ばれています）は、4次元方向の計量を反転させることに対応しているとも言えますが、大ざっぱな幾何学的イメージとしては円錐状の時空を球面状に丸めることに対応しています（下図2参照）。要は、虚時間itの導入によって、4次元の円錐が4次元の球体へと変換されてしまうということです。こうした球体状の時空が実時間宇宙の始まりには存在していたのだ、というのがホーキング=ハートルによる無境界仮説の骨子です。

初期時空がもし球体状のカタチをしているとすると、宇宙の始まりは、ちょうど先の尖った鉛筆の芯をボールペンの芯に変えたときのように、円錐の頂点の先が丸い球面状になっていたことを意味します（図3参照のこと）。このような考え方から、ホーキングは宇宙の始源では、始まりも終わりもないようなエンドレスかつシームレスな世界があったのだと主張します。とすると、このアルケーとしての球面世界は、ビッグバンが起こった場所とビッグクランチの場所が繰り返し相互に繰り返しているような宇宙イメージになってきますし、さらに言えば、この球面上ではどの時空点を取っても全く同等なものになってしまうので、虚時間宇宙上ではどの場所も、宇宙の始まりであり、終わりでもあることになります。これは仏教で言うところの「無始無終（むしむちゅう）」の宇宙像ととてもよく似ていますね。時空上のあらゆる場所、つまり、いつであろうが、どこであろうが、そこは無始無終の久遠の世界が広がっている場所になるということです。「久遠元初（くおんがんじょ）」の出現です。

「久遠とははたらかさず・つくろわず・もとのままという義なり」

「久遠は今に在り、今は即ち久遠なり」

（by 日蓮）

――つづく