4次元時空と4次元空間（2）

　さて、この第四の次元の基底の符号の違いが実質として何を意味するものなのか、それを発見することができれば、僕らは4次元の世界を時間ではなく、空間的な描像として思い描くことができる可能性がでてきます。空間としての4次元認識が可能になってくるということです。

　普通、僕らは第4の空間次元の方向というと、3次元方向の軸が2次元平面に直交していることから、今度は3次元空間に直交する「軸=線分」のイメージでその方向を探そうとします。しかし、いくら探しても僕らの目の前の空間には、タテ、ヨコ、高さ方向としてのx、y、z軸以外見つかりそうにありません。そして、その結果、4次元の方向なんてものは所詮、人間の認識が及ばないものなのだというように結論づけてしまいます。しかし、果たしてそうなのでしょうか。僕らは何かの理由により催眠術にかかっていて、本当はありありと存在している4次元の方向を見逃しているだけかもしれません。OCOTは4次元方向について次のように言います。

　「あなたがたが今持っている3次元認識からこの4次元認識への移行は同じ1次元の差であっても、2次元から3次元へ移るのとはかなり大きな違いがあります」（『人類が神を見る日/アドバンスト・エディション』第1部p.86）

　この言葉に含まれている真意は、おそらく4次元の方向が一般向けの次元の解説書に見られるような、1次元（線）→2次元（面）→3次元（立体）→4次元（超立体）といったような積み上げ式の描像によって為される次元上昇の在り方とはちょっと異なっているということを暗示しています。では、一体どのように違うというのでしょう。4次元空間が何か皆目見当がつかないのであれば、ここは、負の4次元方向とも言える時間軸側からその手がかりを探るしかありません。そこで時間が3次元空間に対してどのような出現の仕方をしているかを見てみましょう。

　このとき時間と空間の媒介となっているのが光です。光は空間を球面状に伝播していくので、3次元空間に埋め込まれた2次元の球面の方程式は時間tを使って次のような式で表すことができます（下図1参照）。

x^2+y^2+z^2=(ct)^2

左辺に移項させると、

x^2+y^2+z^2－(ct)^2=0………（1）

となり、時空における4次元不変距離を示す方程式が出てきます。 

この（1）の式の中のx^2+y^2+z^2と(ct)^2の関係を見てください。x^2+y^2+z^2の方は空間、(ct)^2の方は時間の項になっているのが分かります。空間の項から時間の項を引いたものがゼロになっているわけですから、ここで、空間と時間はヌースの言葉いうところの対化の関係になっていることが分かります。一方がプラスの要素ならば、もう一方はマイナスの要素になっているということです。これは具体的に言うなら、モノから広がる3次元の空間（x^2+y^2+z^2）と4次元としての時間の方向性（(ct)^2）が、互いを相殺するような関係で逆方向に形成されていることを意味しています。僕らがよく、一光年先に見える天球面の情景が1年前のものだと結論づけるのも、光速度を媒介としたこのような空間と時間の関係性から言われていることなのです。

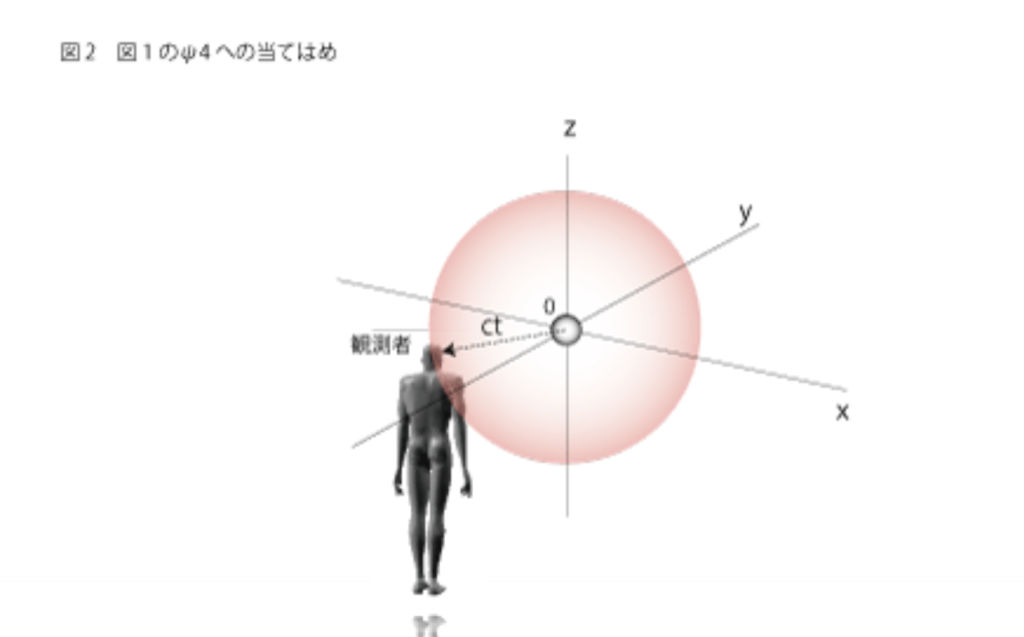
　そこで、この球面のイメージをあえてΨ4の球空間に当てはめてみることにします（下図2）。ここで「あえて」と言ってるのは数学で扱う3次元空間の概念はヌース的にはΨ4とΨ*4の同一化（両者間の反転関係が見えなくさせられているということ）から生まれているものだからです。この同一化が起こる仕組みをヌーソロジーの観点から正確に説明するためには、Ψ9～Ψ10レベルの解説が必要になりますが、ここでは煩雑になることを避けて、”あえて”Ψ4に対応させることにします。 

モノの手前に観測者としての「私の顔」の存在が想定される（これが人間の内面としてのΨ4球空間の半径が持つ意味でした）ことによって、モノと「わたし」は分離を余儀なくされ、その引き裂かれた距離は、空間的には（x^2+y^2+z^2）の平方根、時間的には（(ct)^2）の平方根であるctに相当してくることが分ります。このctの意味するところは、観測者に見えているモノは決して現在・現時点でのモノではなく、モノから放れた光が観測者の顔に届くまでに幾ばくかの時間を要するので、わずかに過去の姿になってますよ、というくらいの意味です。

　さて、今度はこのΨ4の球空間をΨ3側へと反転させてみましょう。この反転した球空間の半径は明らかにctでは表せないものであることが分ります。というのも、この反転操作は時間的には時間自体を裏返すことと同じ意味を持つからです。時間の反転は物理学の表記では時間tに虚数iを掛けることに相当し、虚時間と呼ばれています。この虚時間は時間tに虚数 i をかけて、t→ i t で表すことができます。すると、反転した球空間Ψ3の球面の方程式は、

x^2+y^2+z^2－(cit)^2=0

となり、整理すると、

x^2+y^2+z^2＋(ct)^2=0………（こちらはΨ3とΨ*3の同一化が作り出しているものと考えられます）

となります。

　ctを第4の次元と考えた場合、これは4次元空間に埋め込まれた半径ゼロの3次元球面という高次の球面として解釈することができます。まぁ、半径ゼロだったら球面とも呼べないのて、3次元球面が半径ゼロにまで潰された状態と言い換えたほうがいいのかもしれません。いずれにしろ、反転した球空間Ψ3側は時間が空間と同等の存在となって、”時間が存在しなくなる”わけです。その意味でこれは光速度状態そのものと言っていい場所になります（光速度では時計が止まるということ）。

　ここで以前に行なったΨ3の球空間をイメージするためのワークを思い出して下さい。絶えずモノを見つめながら、観測者がその周囲を回転したときに、モノの中心とその背景面方向に向かっていると想定される視線の貫きが作る球空間……それがΨ3の球空間の意味でした。そして、その方向は奥行きが一点で同一視されているために中心点とほとんど見分けがつかない、という言い方をしたと思います。どうでしょうか。この式のイメージにかなり似ていませんか？

――つづく。